Adaptive exploration of physical systems

FLEX: an Adaptive Exploration Algorithm for Nonlinear Systems

Matthieu Blanke, Marc Lelarge

Inria Paris, DI ENS, PSL Research University

ICML2023 Paper Code Demo

Abstract

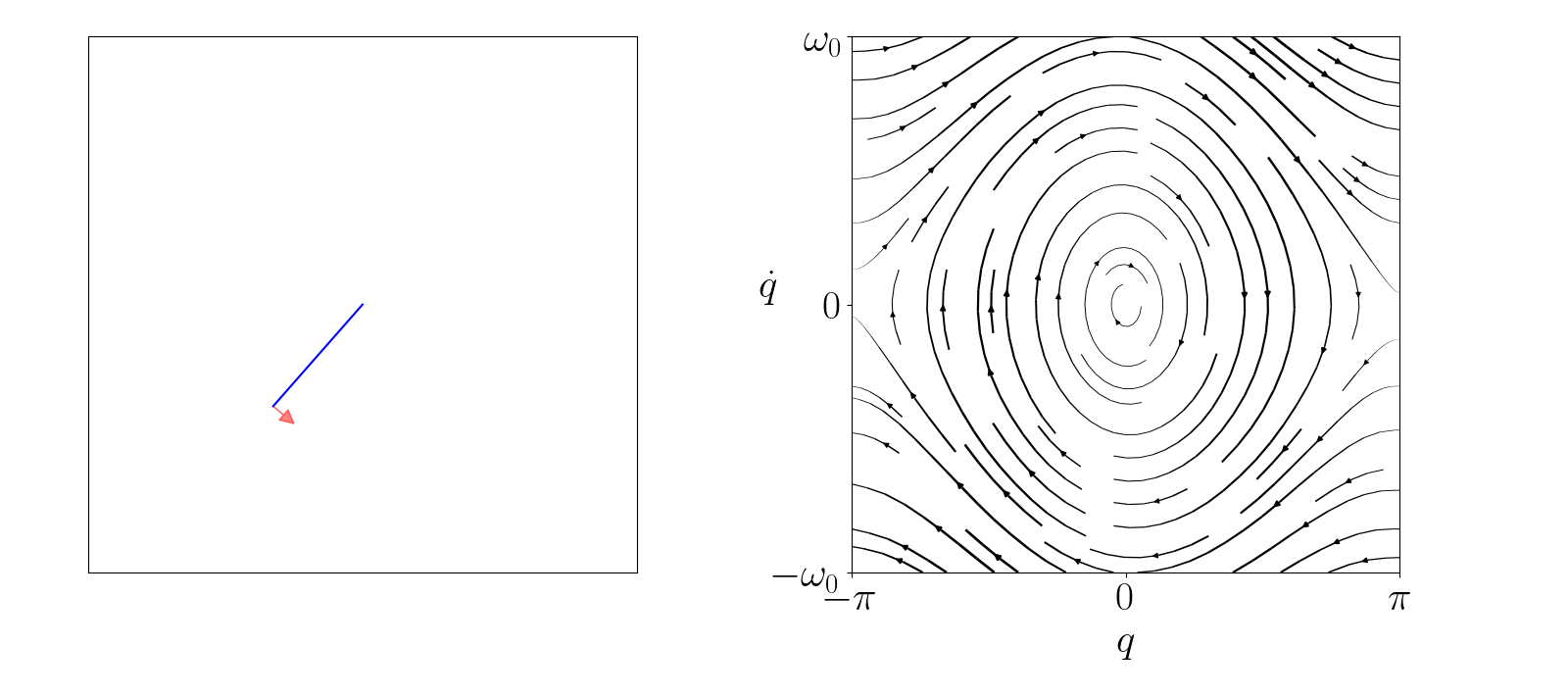
Model-based reinforcement learning is a powerful tool, but collecting data to fit an accurate model of the system can be costly. Exploring an unknown environment in a sample-efficient manner is hence of great importance. However, the complexity of dynamics and the computational limitations of real systems make this task challenging. In this work, we introduce FLEX, an exploration algorithm for nonlinear dynamics based on optimal experimental design. Our policy maximizes the information of the next step and results in an adaptive exploration algorithm, compatible with generic parametric learning models and requiring minimal resources. We test our method on a number of nonlinear environments covering different settings, including time-varying dynamics. Keeping in mind that exploration is intended to serve an exploitation objective, we also test our algorithm on downstream model-based classical control tasks and compare it to other state-of-the-art model-based and model-free approaches. The performance achieved by FLEX is competitive and its computational cost is low.

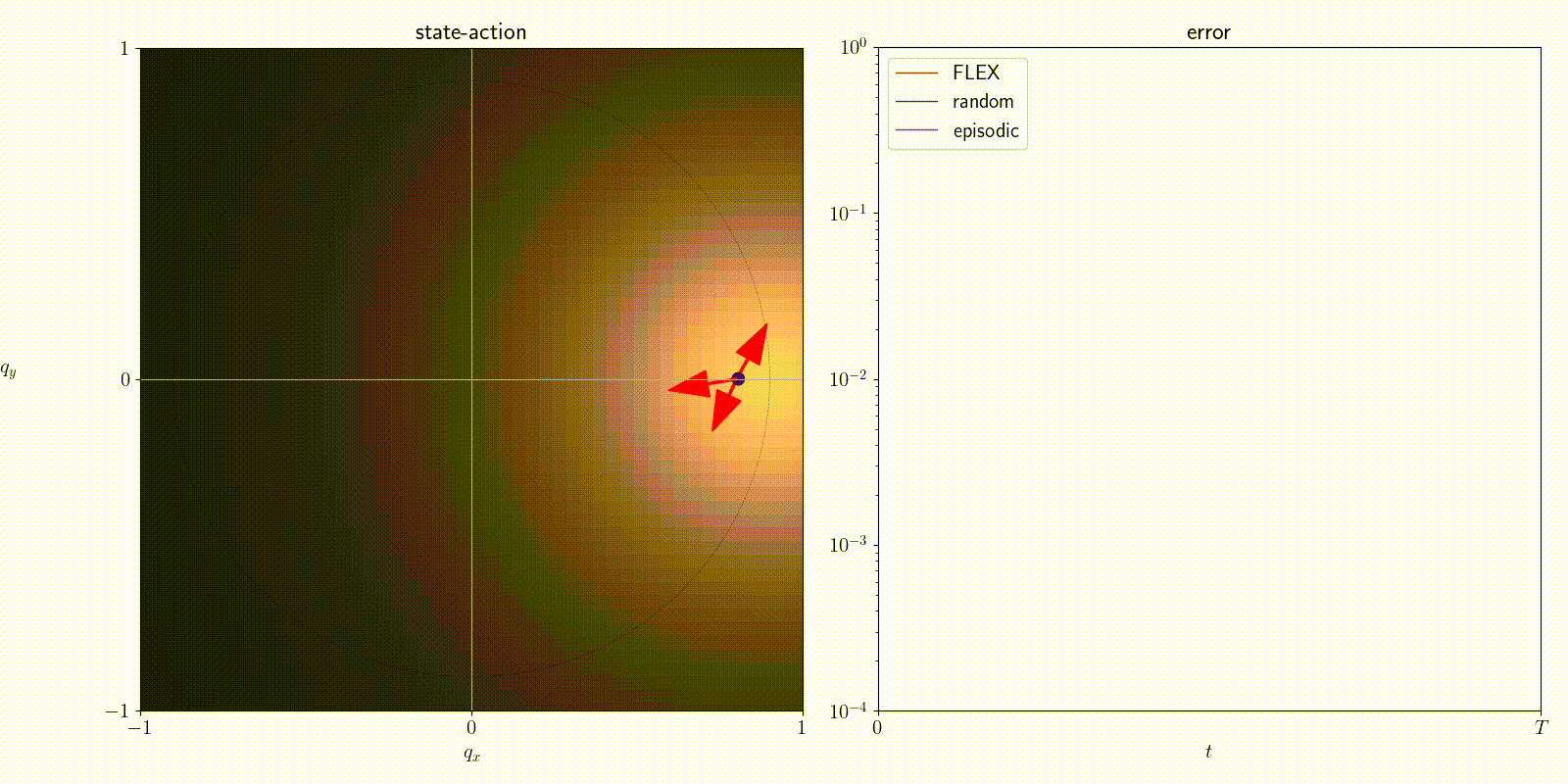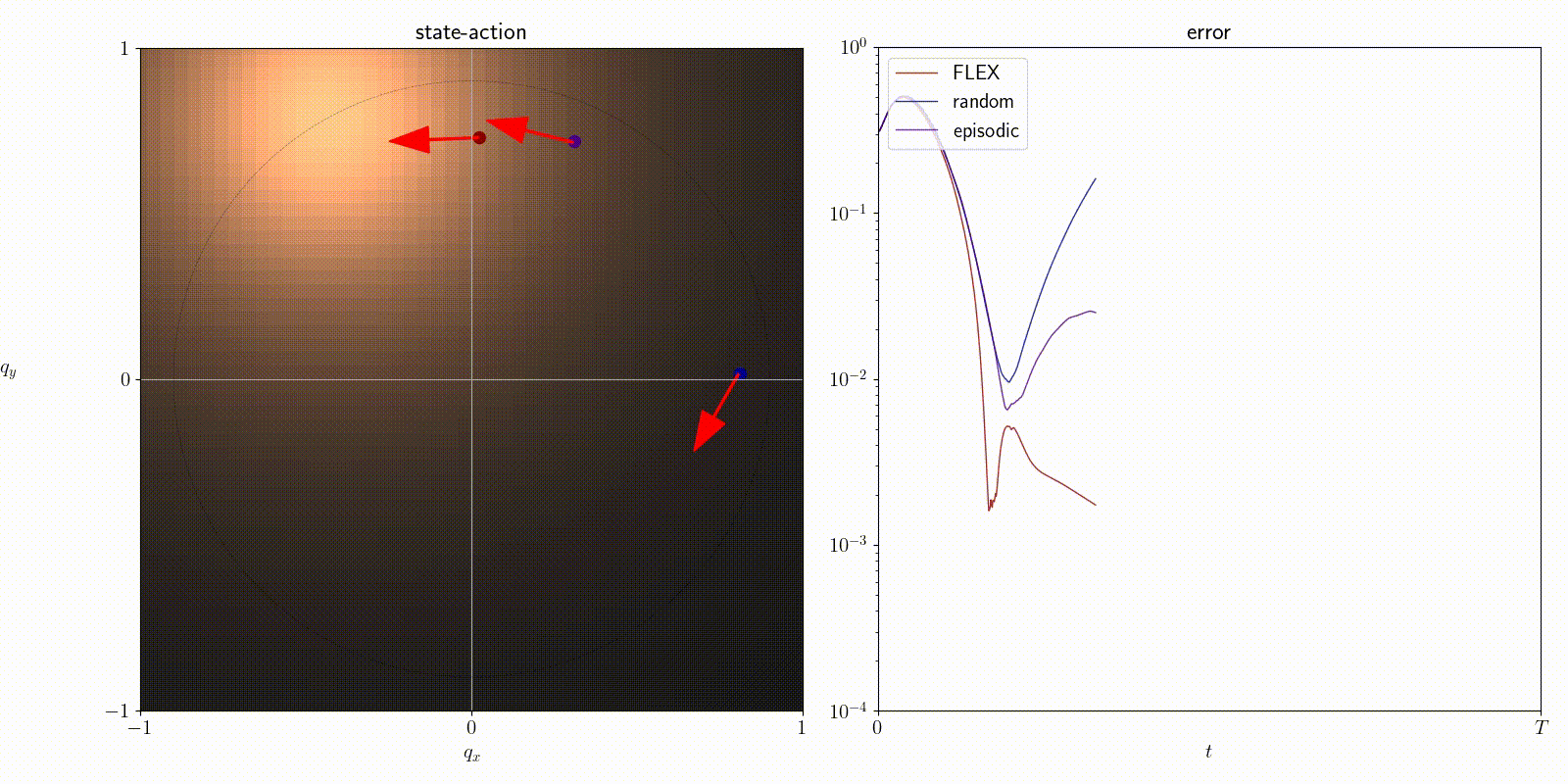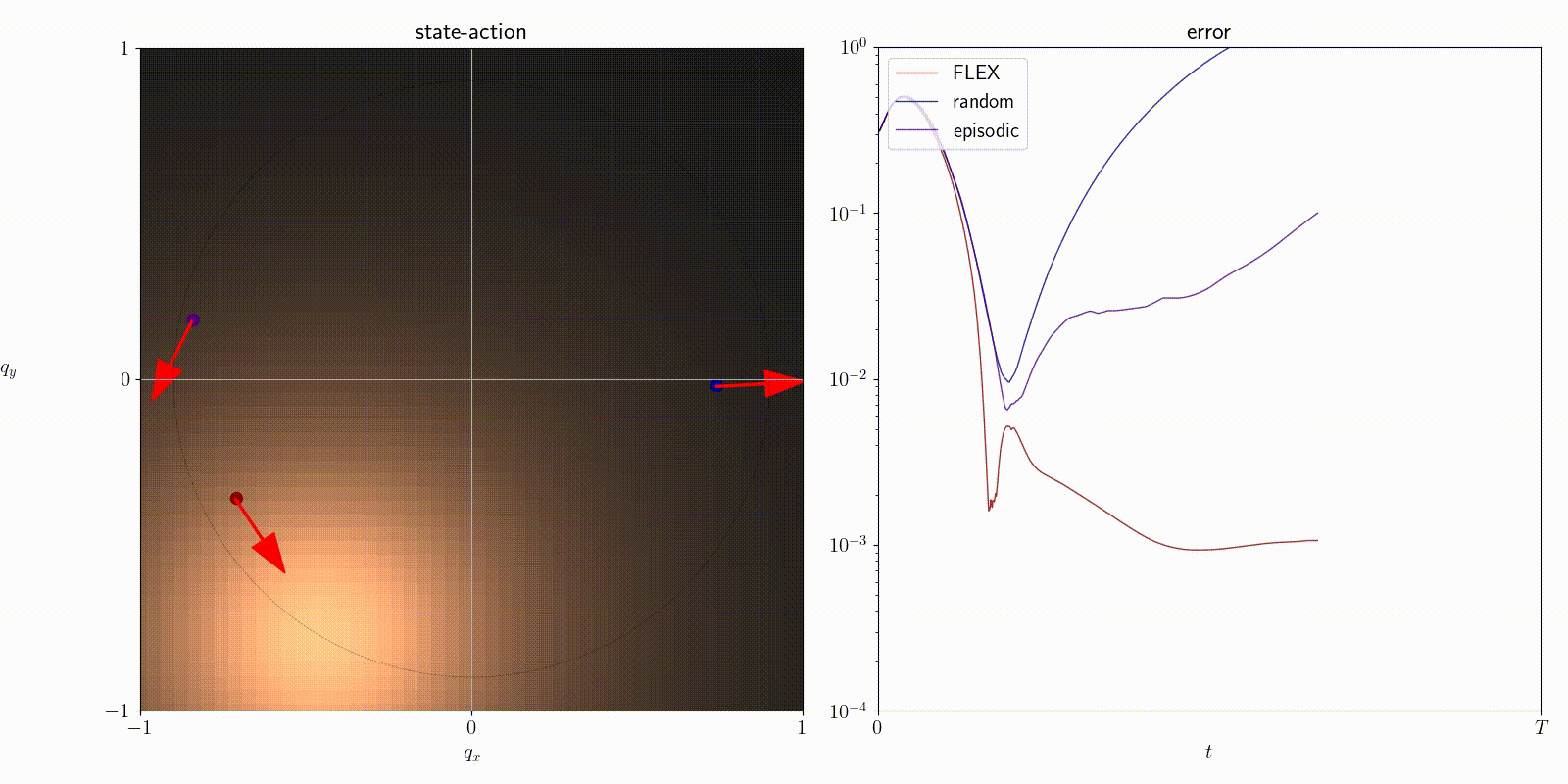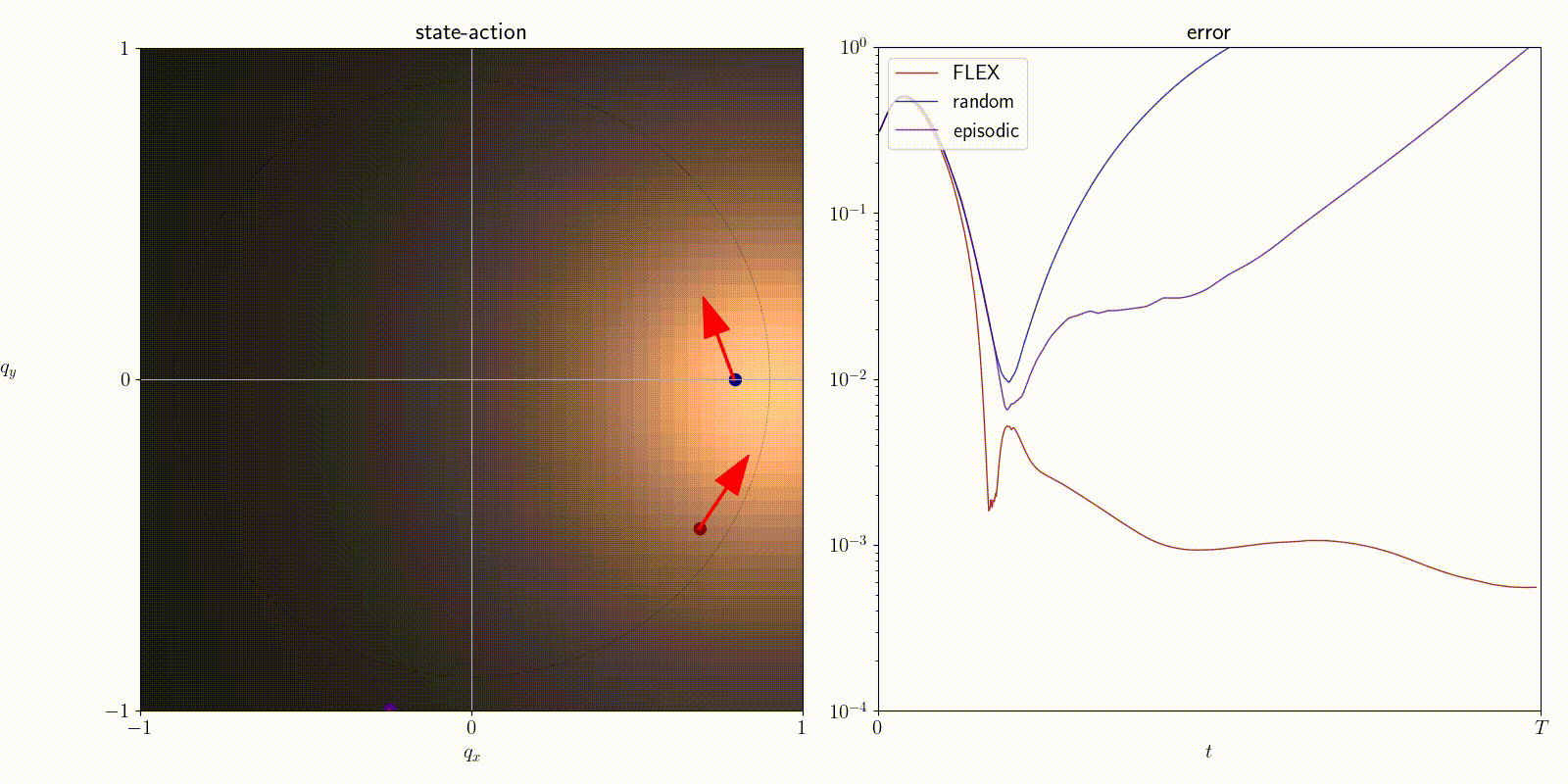
Classical control environments

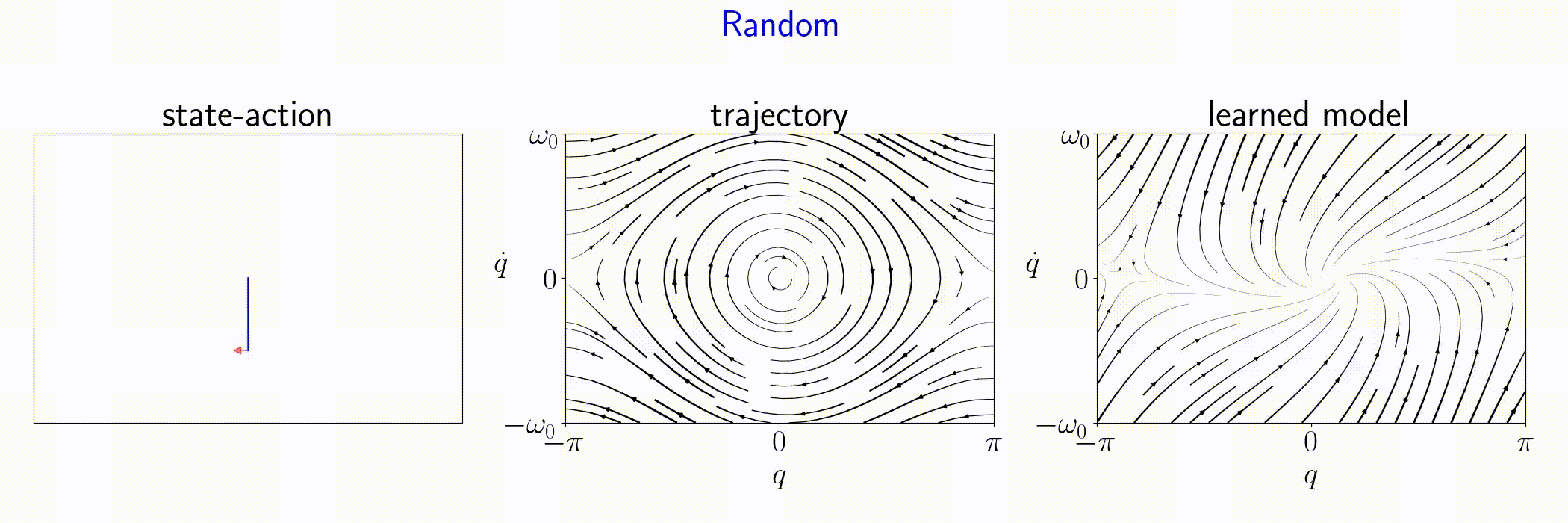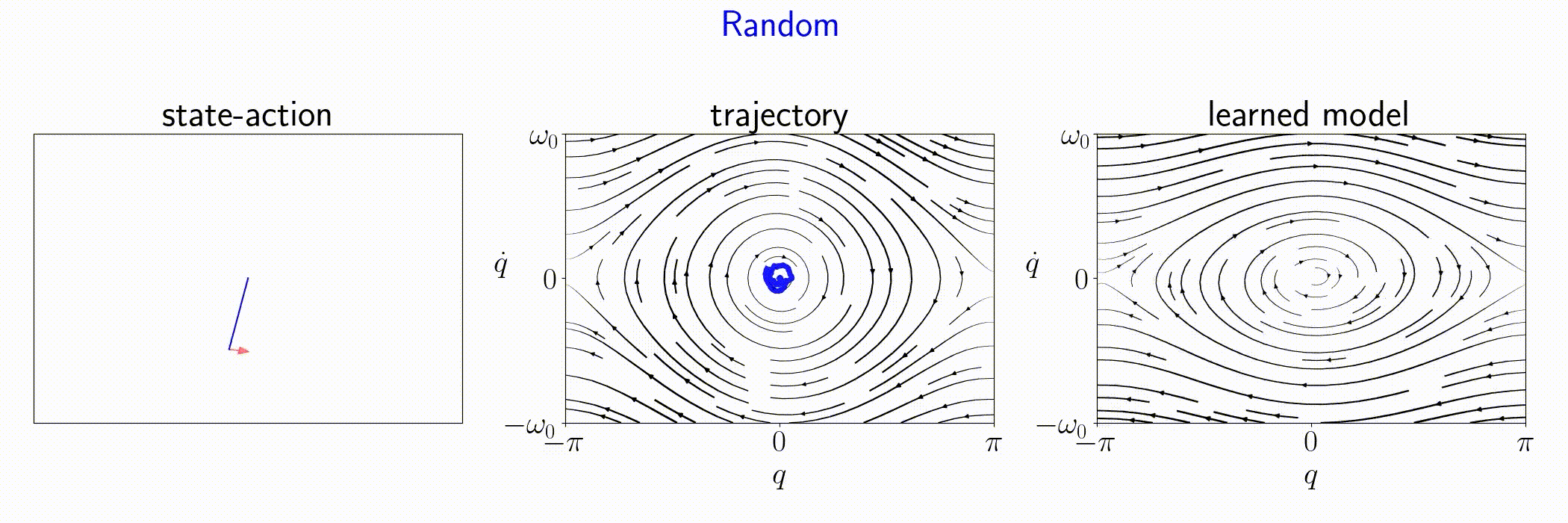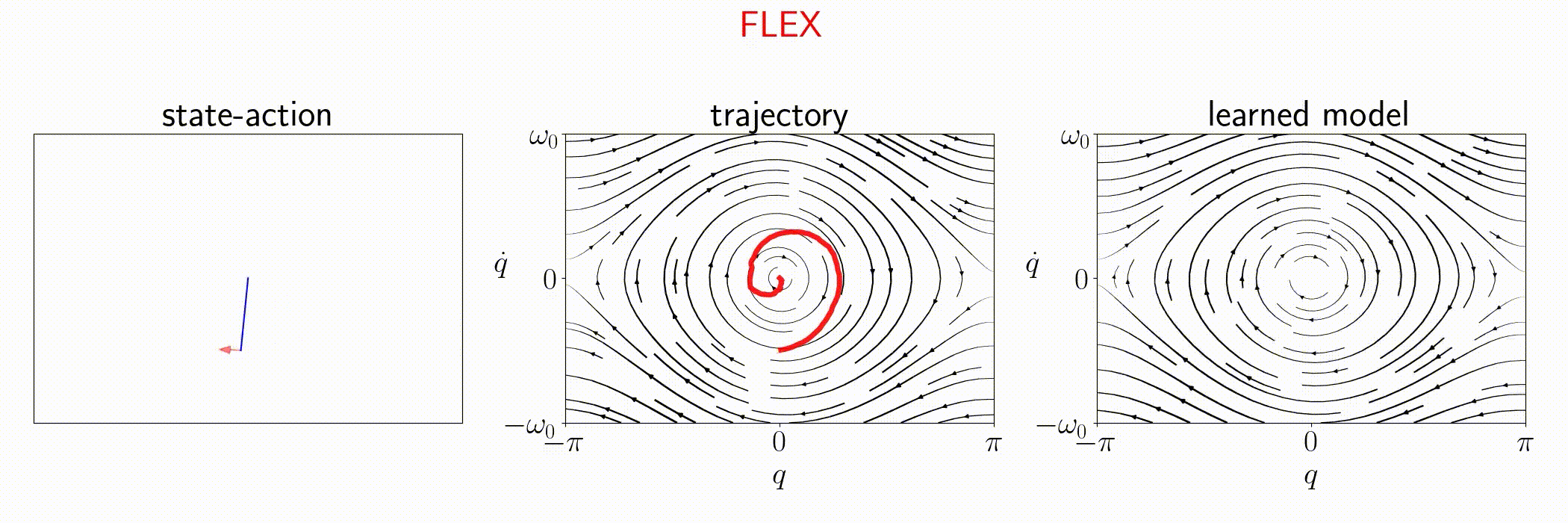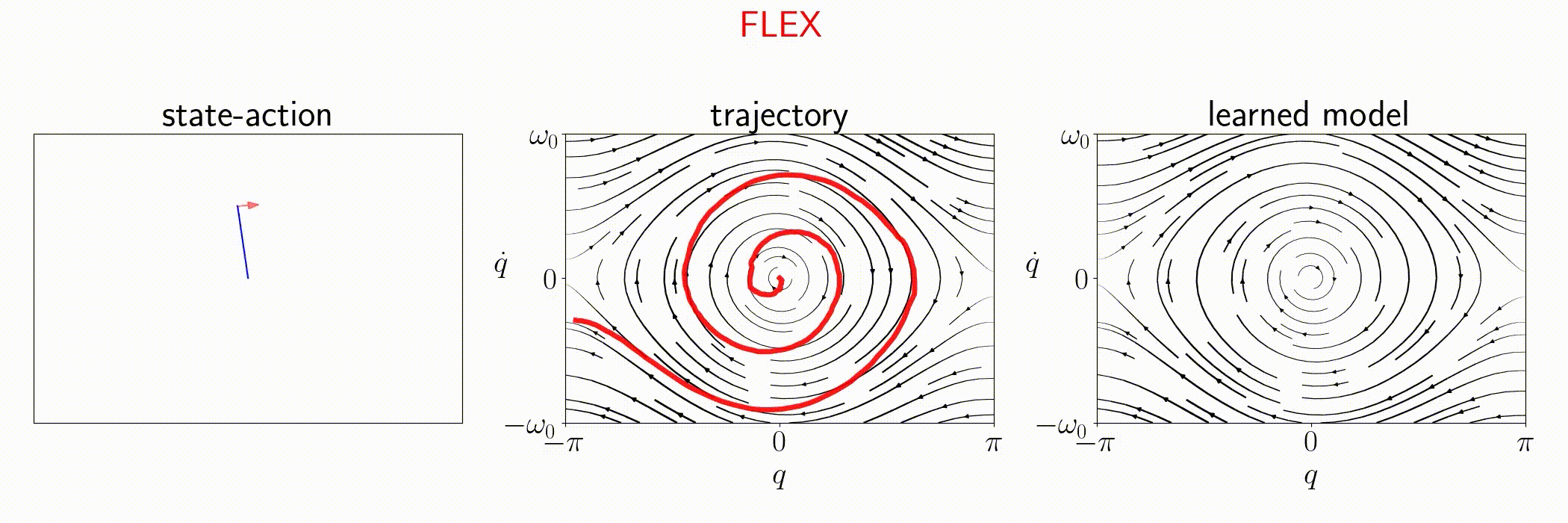
We compare FLEX with baselines on a number of classical control nonlinear environments.

Pendulum

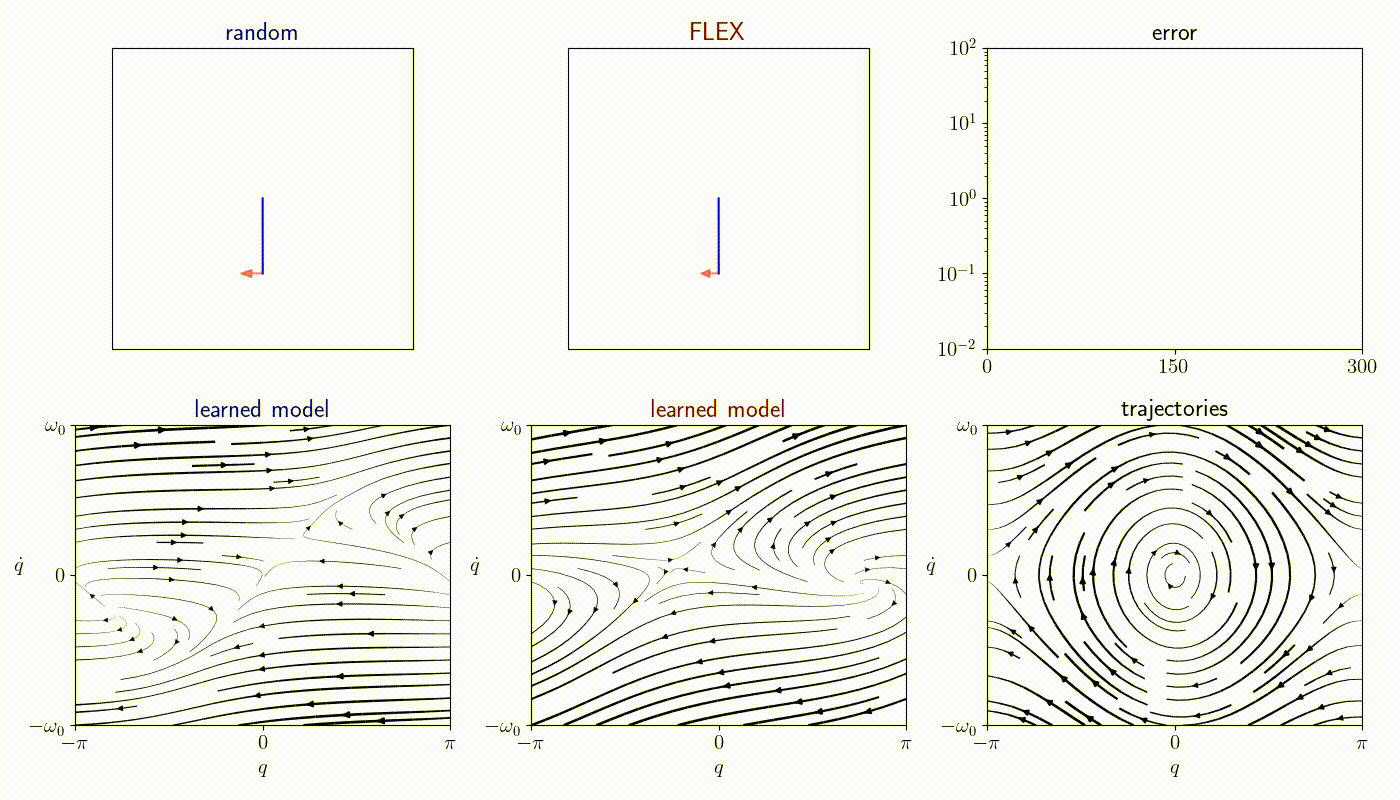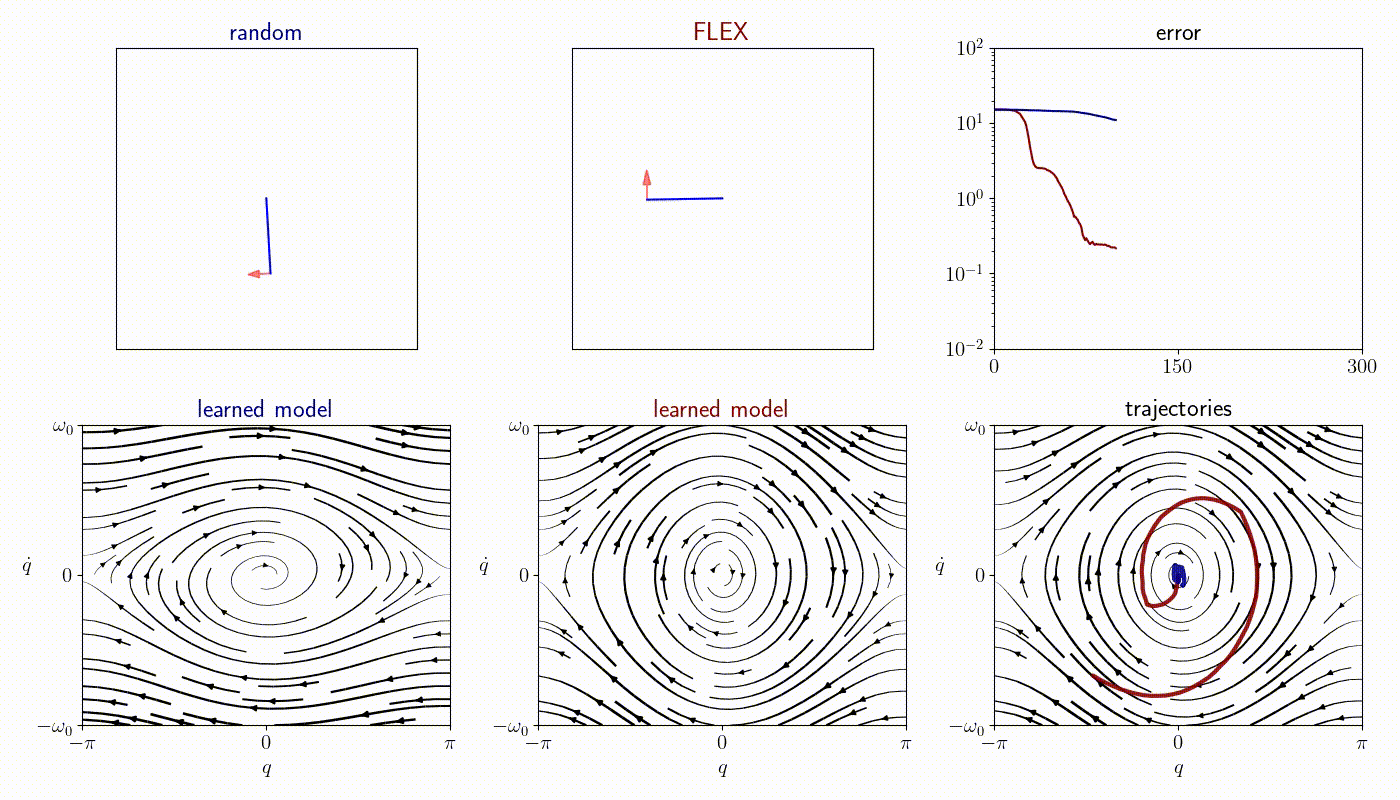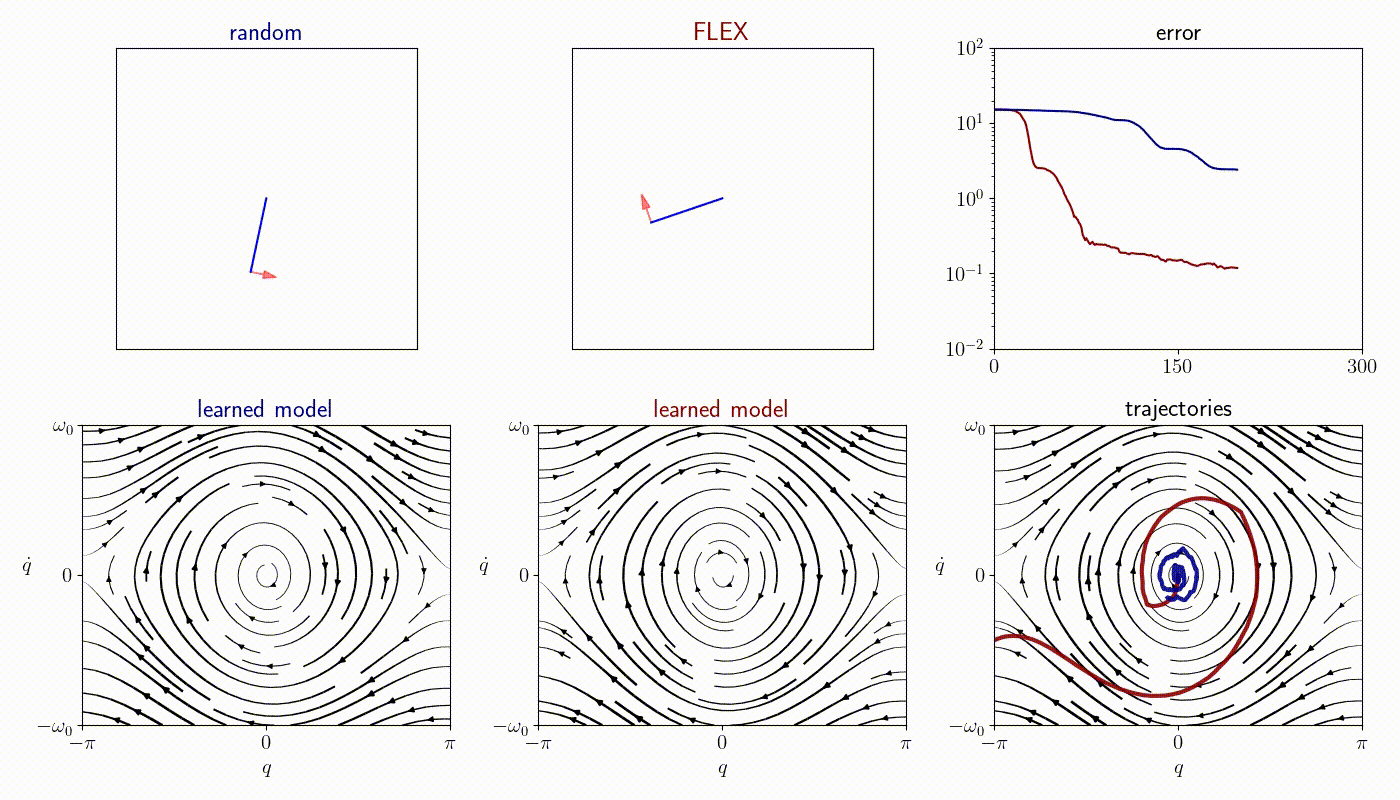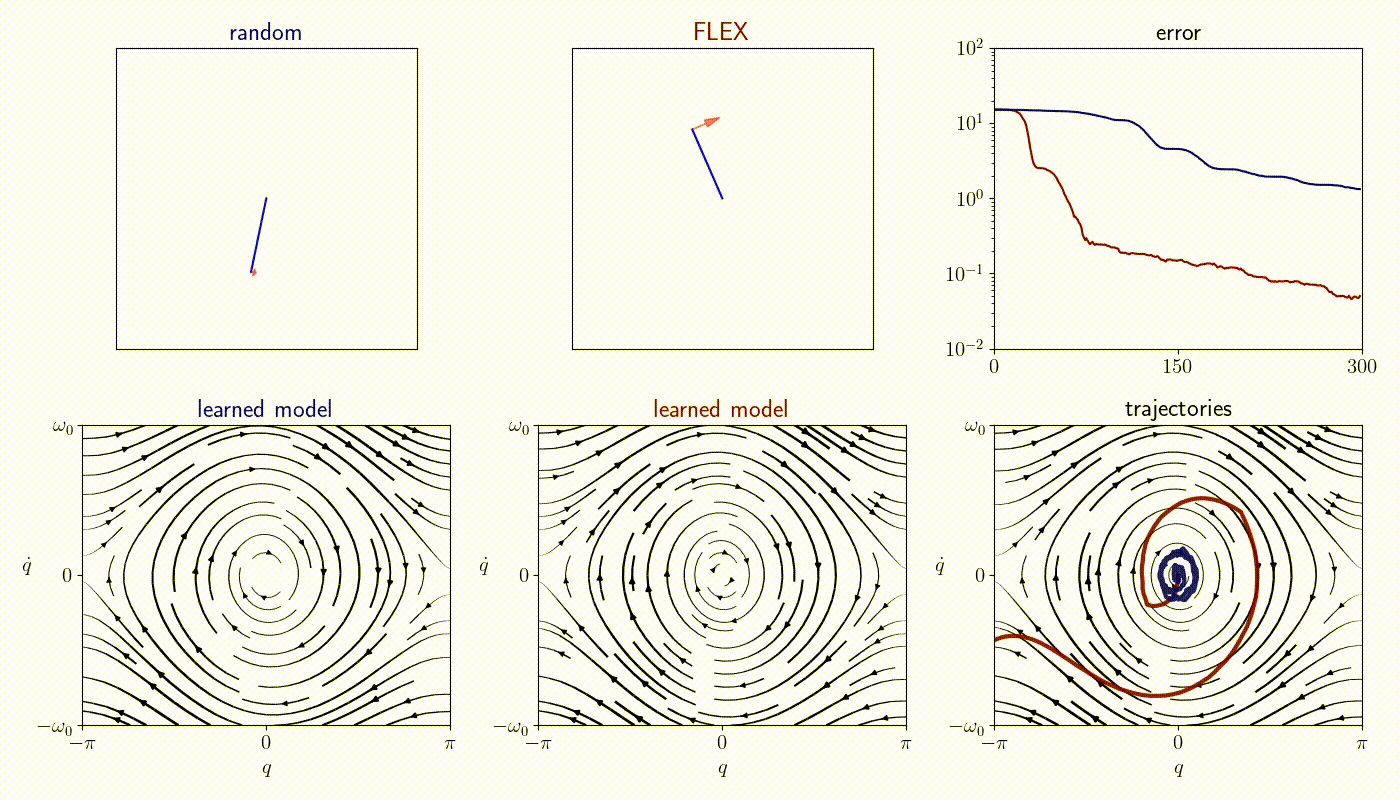
Cartpole

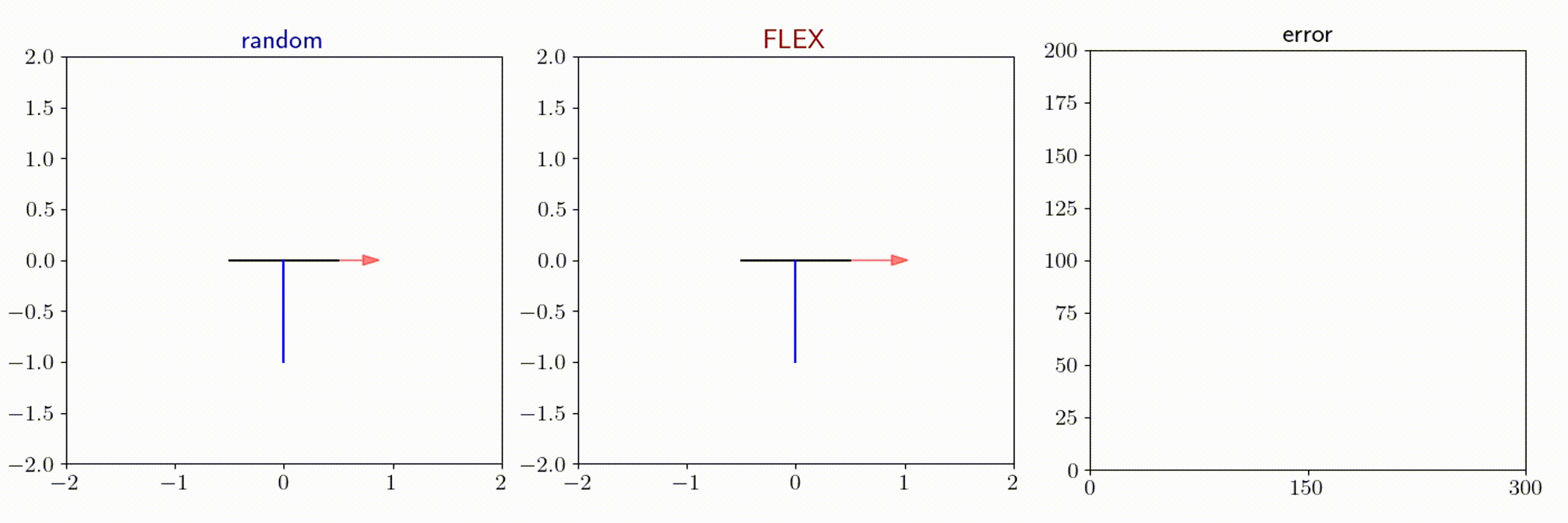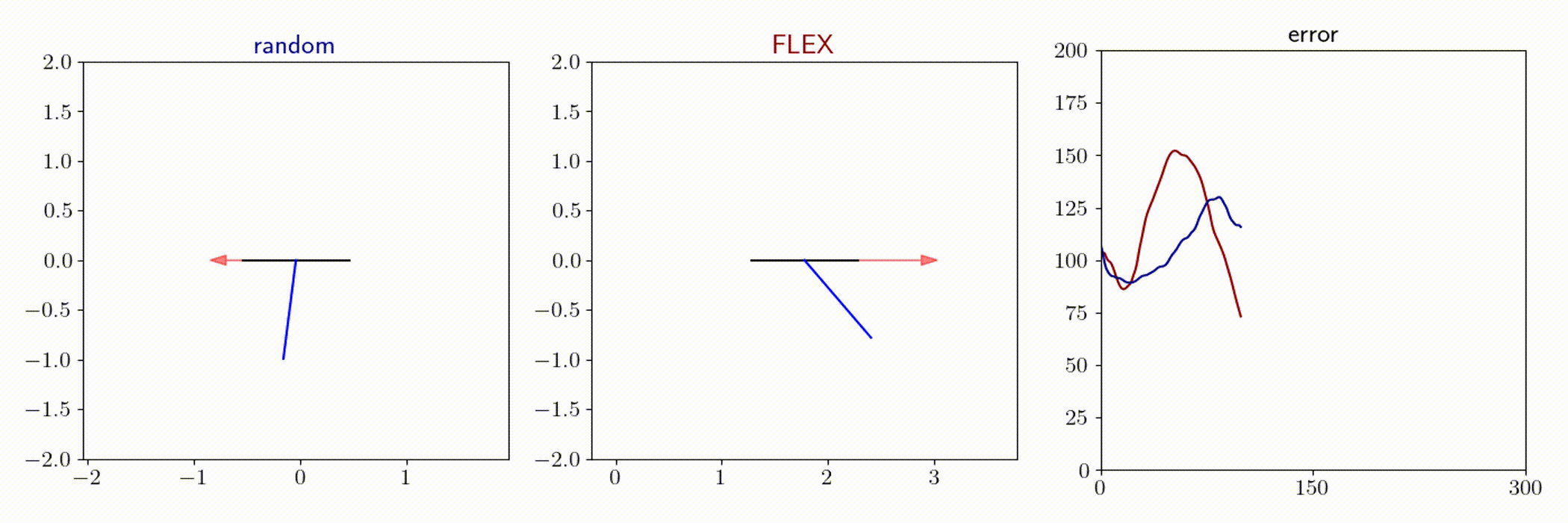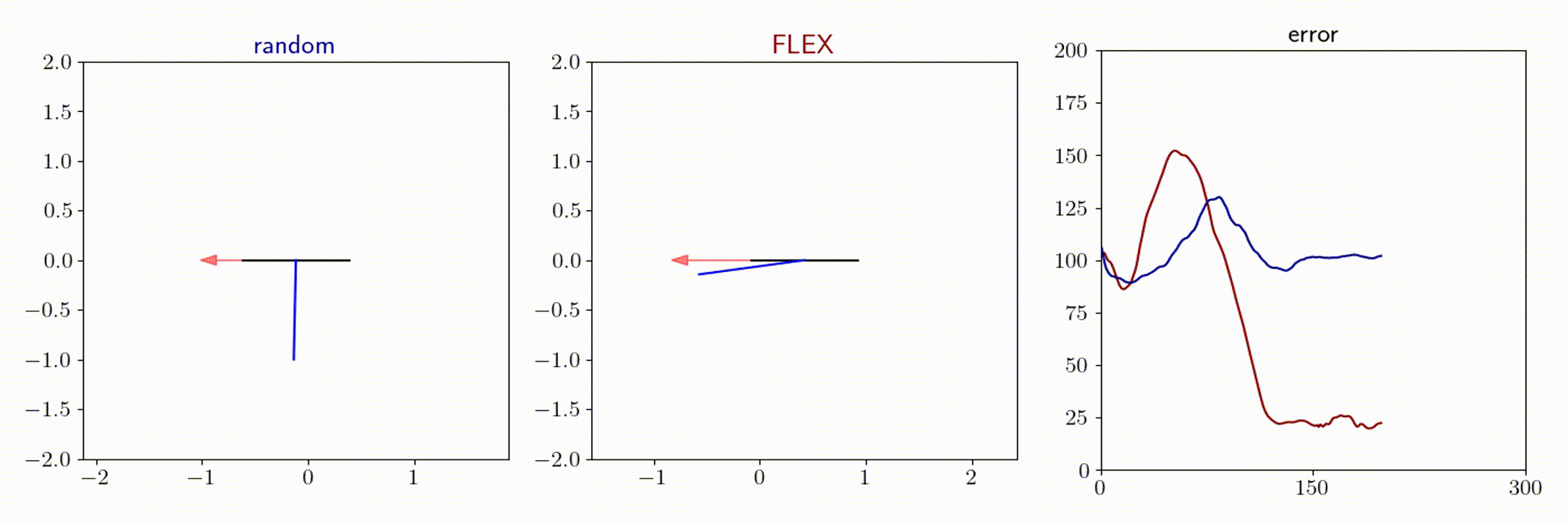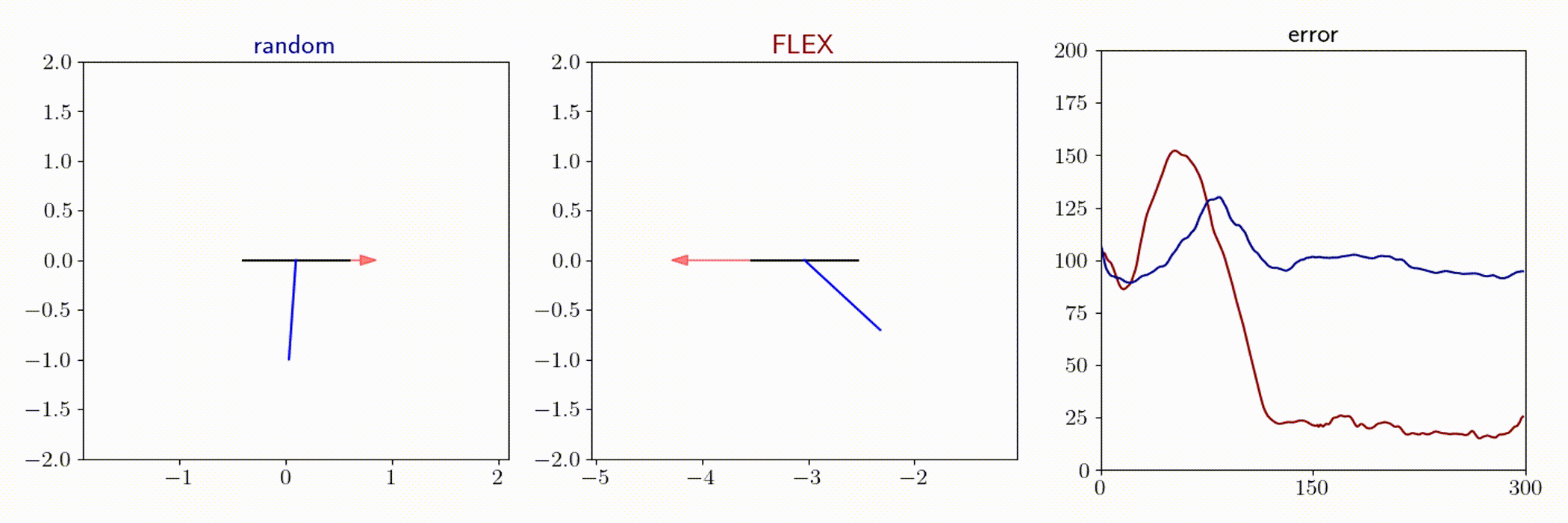
Quadrotor

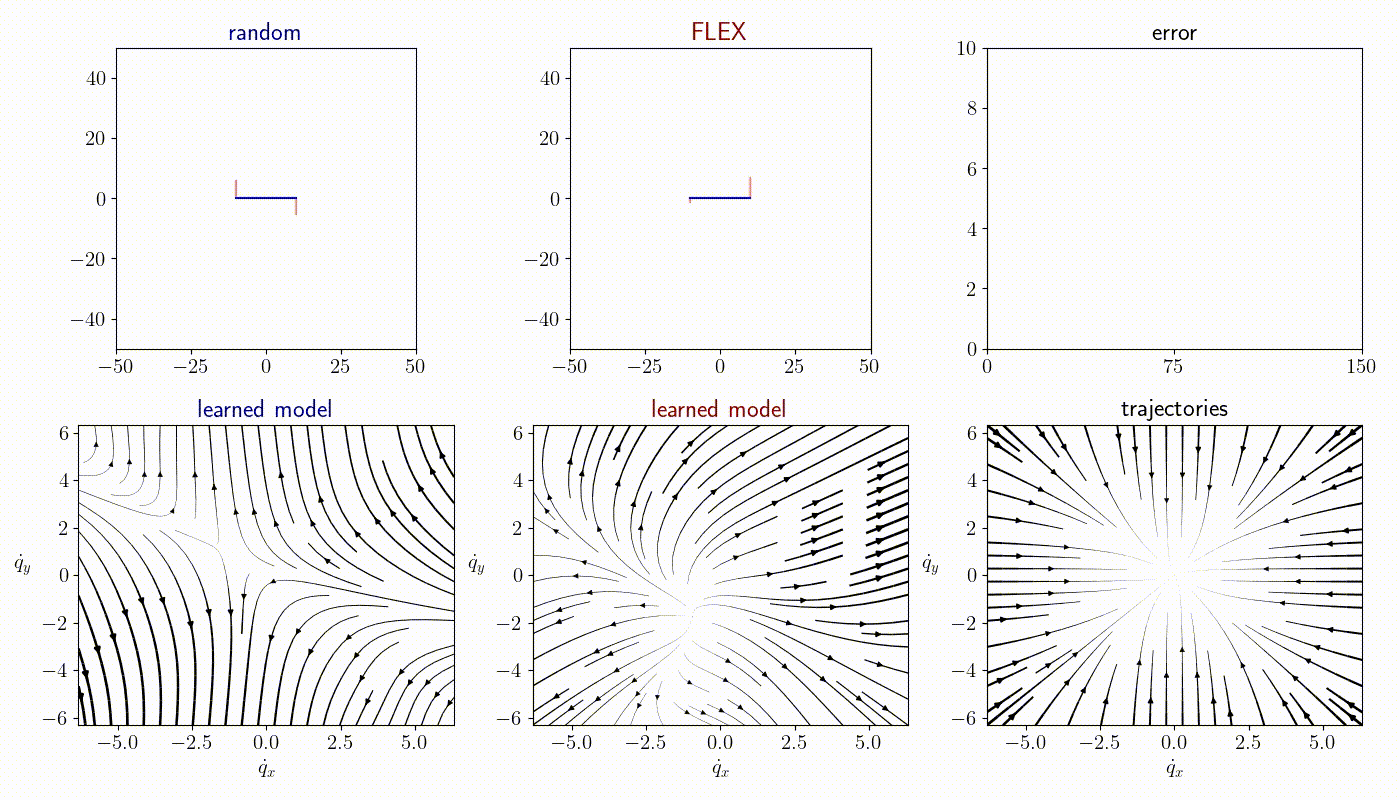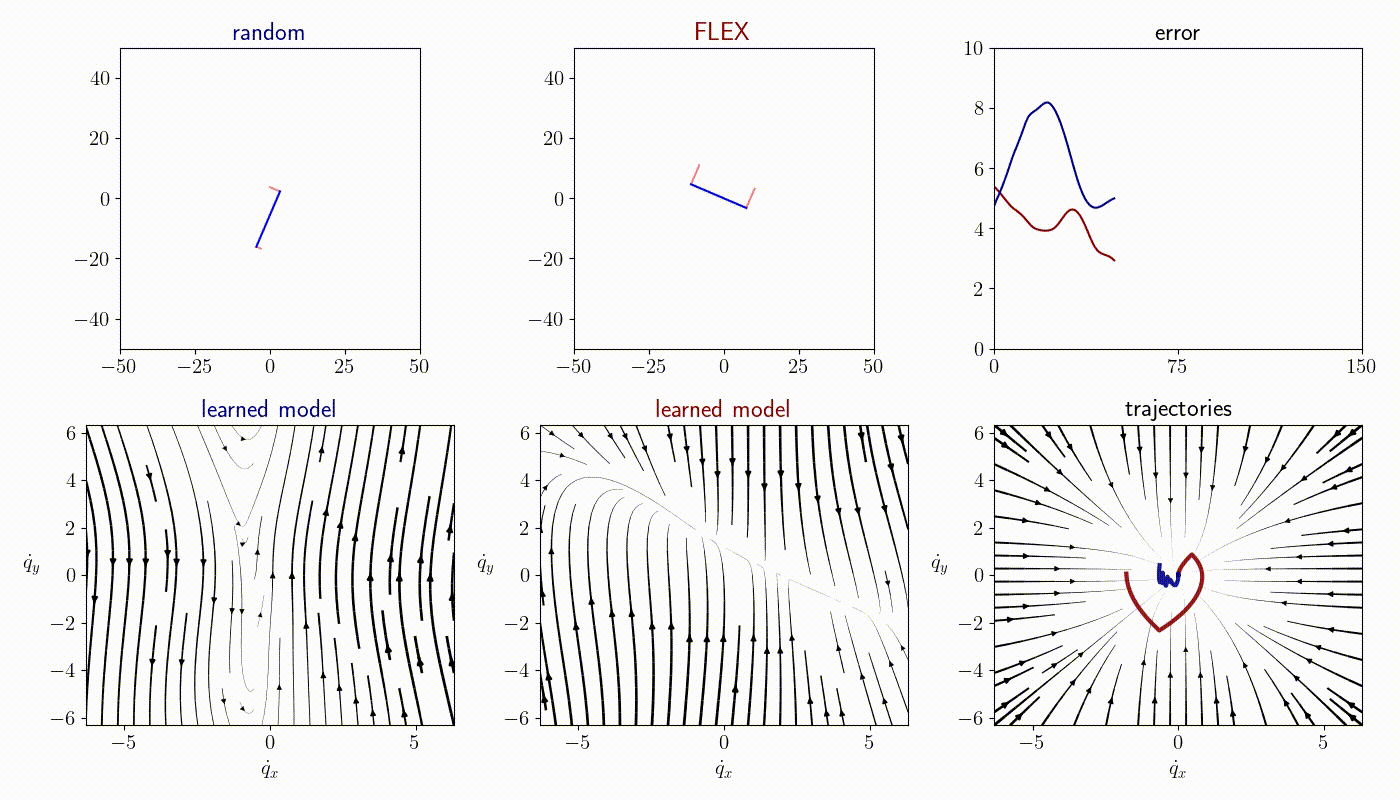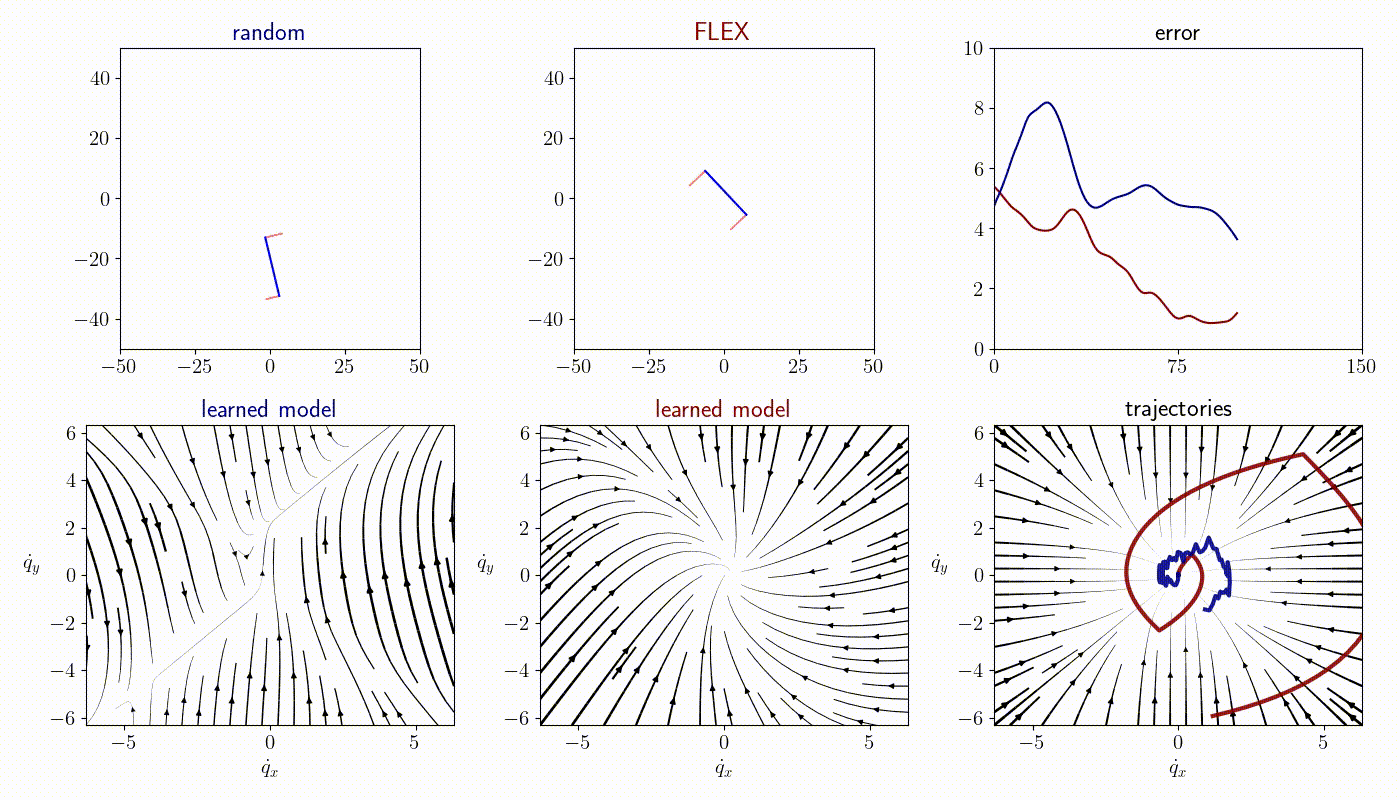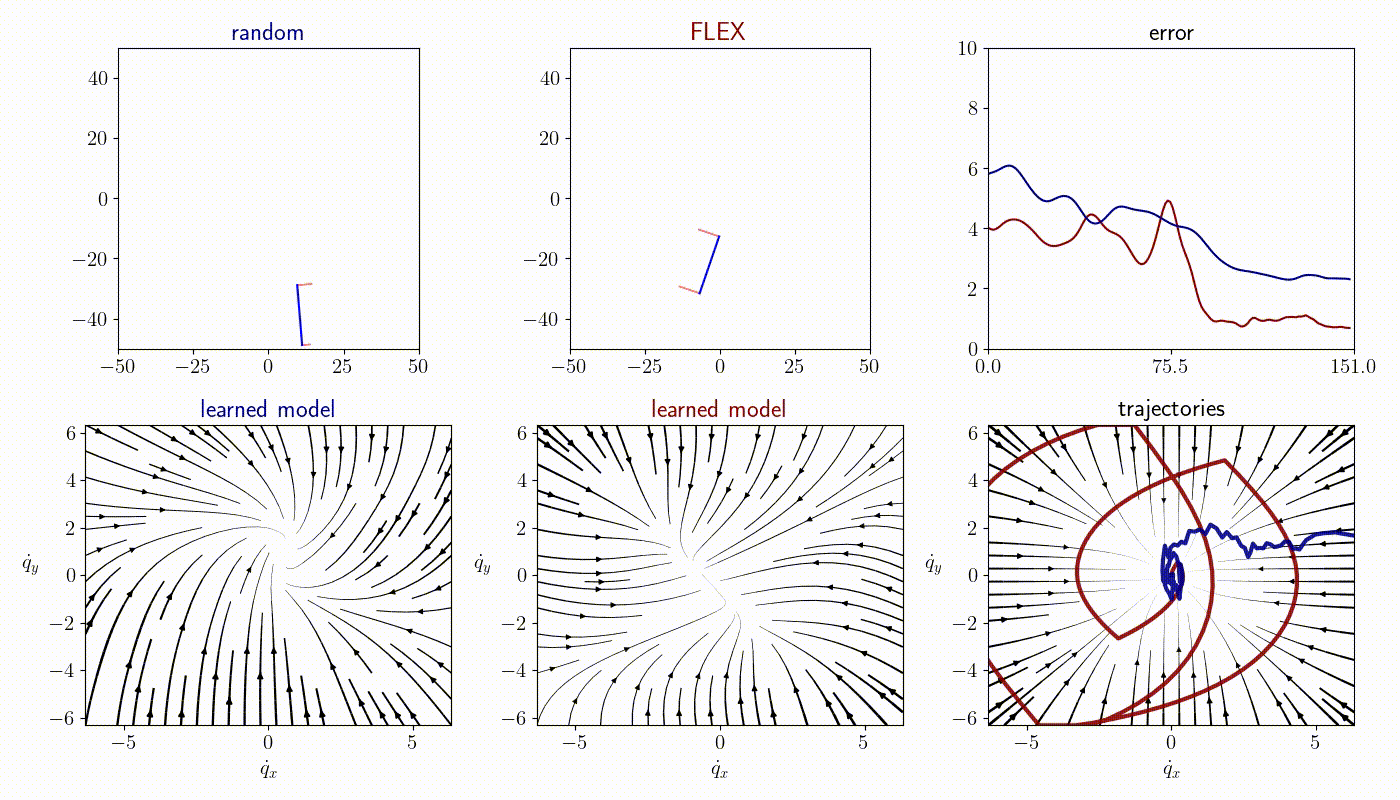
Time-varying dynamics

FLEX is an adaptive policy, allowing the agent to accomodate to new observations at each time step. As a consequence, FLEX can track time-varying dynamics.

Citation

To cite this work, please use the following references.

Blanke, M., & Lelarge, M. (2023). FLEX: an Adaptive Exploration Algorithm for Nonlinear Systems. International Conference on Machine Learning.

@article{blanke2023flex,
  title={FLEX: an Adaptive Exploration Algorithm for Nonlinear Systems},
  author={Blanke, Matthieu and Lelarge, Marc},
  journal={International Conference on Machine Learning},
  year={2023}
}

A parallel with the historical meaning of exploration

A sailor wants to explore the world aboard his boat. How should he choose his course in order to map the world as quickly as possible, based on what he observes along the way? This question sums up the problem of exploration, which arises in a similar way in the learning of physical systems, where the aim is to learn the dynamics of the system with as few experiments as possible.